Dalam dunia penelitian, memilih sampel dari populasi bukan hanya soal “mengambil secara acak” dan selesai. Kadang, keacakan saja tidak cukup untuk mewakili keberagaman dalam populasi. Misalnya, ketika sebuah populasi terdiri dari kelompok-kelompok yang sangat berbeda, seperti laki-laki dan perempuan, atau mahasiswa S1 dan S2. Nah, dalam kasus seperti ini, metode yang disebut Stratified Random Sampling hadir sebagai solusi yang lebih adil dan representatif.
Metode ini melibatkan pembagian populasi menjadi beberapa strata, yaitu subkelompok yang punya karakteristik homogen di dalamnya. Setelah strata terbentuk, pengambilan sampel dilakukan secara acak di masing-masing strata. Pendekatan ini sangat bermanfaat dalam berbagai bidang—mulai dari penelitian sosial, survei kesehatan, hingga pendidikan—karena mampu menurunkan kesalahan pengambilan sampel dan meningkatkan akurasi hasil.
Pengertian Stratified Random Sampling
Stratified Random Sampling adalah metode pengambilan sampel di mana populasi dibagi terlebih dahulu ke dalam subkelompok homogen yang disebut strata. Setelah itu, dilakukan random sampling secara independen di masing-masing strata. Tujuan dari metode ini adalah untuk memastikan bahwa setiap kelompok penting dalam populasi mendapatkan representasi yang adil dalam sampel akhir.
Menurut William G. Cochran dalam bukunya Sampling Techniques (1977), “stratification reduces the sampling error by controlling variability within strata.” Artinya, dengan memisahkan populasi ke dalam strata yang lebih seragam, variasi dalam tiap kelompok dapat dikendalikan lebih baik, sehingga hasil analisis menjadi lebih stabil dan dapat diandalkan.
Metode ini juga sangat fleksibel dan dapat diterapkan pada populasi dengan keragaman tinggi. Misalnya, dalam studi kepuasan pelanggan nasional, kita bisa membagi responden berdasarkan provinsi, jenis kelamin, atau jenis layanan yang digunakan, lalu mengambil sampel acak dari setiap kelompok tersebut.
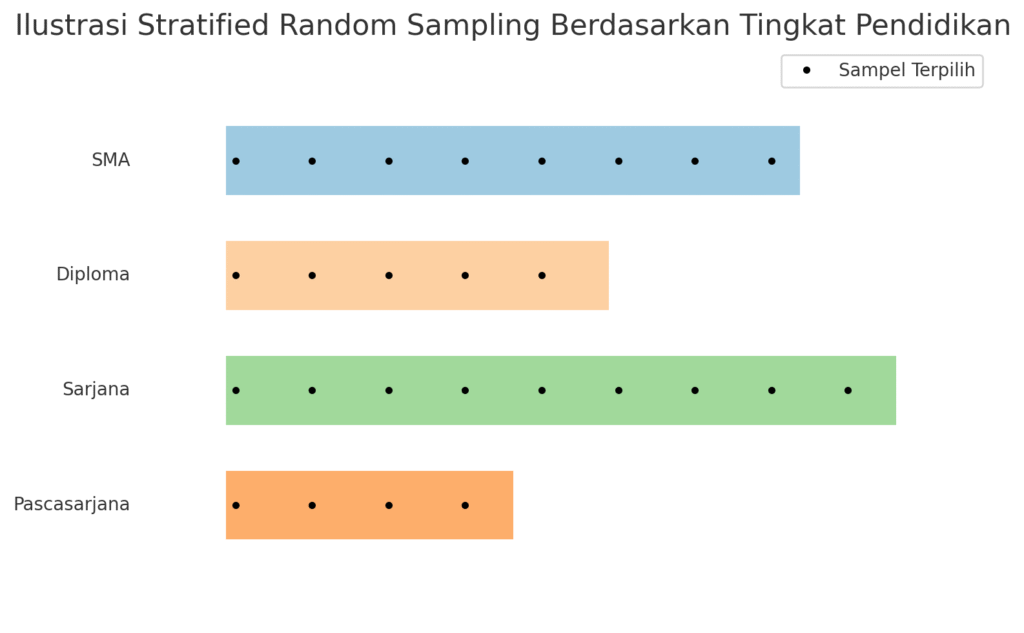
Populasi dan Elemen dalam Stratified Sampling
Dalam statistik, istilah populasi merujuk pada seluruh kelompok yang menjadi objek penelitian—bisa berupa manusia, hewan, produk, atau data lainnya. Sedangkan elemen adalah unit terkecil dari populasi, misalnya satu orang responden, satu perusahaan, atau satu rumah tangga.
Dalam Stratified Sampling, elemen-elemen ini dikelompokkan ke dalam strata berdasarkan karakteristik tertentu yang dianggap relevan dengan tujuan penelitian. Karakteristik ini bisa sangat beragam: usia, jenis kelamin, tingkat pendidikan, pendapatan, hingga lokasi geografis. Yang penting, masing-masing strata harus bersifat homogen—artinya, elemen di dalamnya memiliki kemiripan yang tinggi satu sama lain.
Misalnya, dalam survei kepuasan pelanggan sebuah perusahaan yang punya 5 cabang, peneliti bisa membagi populasi pelanggan menjadi lima strata berdasarkan cabang. Dengan begitu, hasil dari setiap cabang akan terwakili dalam laporan akhir, dan keputusan bisnis bisa diambil lebih spesifik dan tepat sasaran.
Konsep Dasar dan Tujuan Stratifikasi
Stratifikasi bukan hanya sekadar membagi populasi ke dalam kelompok-kelompok. Konsep ini lahir dari kebutuhan untuk meningkatkan kualitas hasil pengambilan sampel. Dengan memahami alasan di balik penggunaan stratified sampling, sobat bisa melihat betapa pentingnya strategi ini dalam praktik statistik.
Berikut beberapa tujuan utama dari stratifikasi:
- Mengurangi variansi antar sampel: Karena setiap strata terdiri dari elemen yang seragam, perbedaan antar elemen dalam satu strata menjadi kecil. Ini membantu menurunkan variansi estimasi.
- Meningkatkan representasi kelompok minoritas: Dalam simple random sampling, kelompok kecil mungkin luput. Dengan stratifikasi, kelompok kecil tetap bisa terwakili secara proporsional.
- Meningkatkan efisiensi statistik: Dengan desain yang baik, peneliti bisa mendapatkan hasil yang lebih presisi tanpa harus meningkatkan ukuran sampel secara signifikan.
Penerapan metode ini sangat relevan di dunia nyata. Misalnya, dalam pemilu, pemilih bisa dibagi berdasarkan wilayah geografis, usia, atau tingkat pendidikan. Dengan stratifikasi, hasil survei opini publik menjadi lebih akurat karena setiap kelompok penting dalam masyarakat bisa terwakili secara adil. Hal serupa juga berlaku dalam survei sosial berskala nasional yang ingin mengetahui kondisi rumah tangga di berbagai provinsi di Indonesia.
Ilustrasi Penggunaan Stratified Sampling
Untuk mempermudah pemahaman, mari kita ambil sebuah contoh nyata. Sebuah universitas ingin melakukan survei untuk mengetahui tingkat stres mahasiswa. Alih-alih langsung mengambil sampel dari seluruh mahasiswa secara acak, pihak universitas memutuskan menggunakan metode stratified sampling.
Mahasiswa dibagi ke dalam tiga strata berdasarkan jenjang studi:
- S1 (Sarjana)
- S2 (Magister)
- S3 (Doktoral)
Dari setiap strata tersebut, dilakukan pengambilan sampel secara acak. Dengan begitu, mahasiswa dari setiap jenjang akan terwakili dan hasil survei bisa memberikan gambaran yang lebih menyeluruh mengenai tingkat stres berdasarkan tingkat pendidikan.
| Strata | Jumlah Mahasiswa | Jumlah Sampel |
|---|---|---|
| S1 | 1000 | 100 |
| S2 | 300 | 30 |
| S3 | 100 | 10 |
Contoh alokasi sampel pada tiap strata di universitas.
Prosedur dan Rumus Stratified Random Sampling
Dalam menerapkan stratified sampling, ada beberapa langkah sistematis yang bisa sobat ikuti agar prosesnya berjalan dengan baik dan hasilnya akurat:
- Tentukan kriteria strata: Pilih karakteristik relevan yang akan digunakan untuk membagi populasi, misalnya jenis kelamin, usia, wilayah, atau jenjang pendidikan.
- Bagi populasi ke dalam strata: Pastikan setiap elemen hanya masuk ke satu strata dan tidak tumpang tindih.
- Tentukan jumlah sampel tiap strata: Bisa dengan metode proporsional, disproposional, atau optimum allocation (dibahas nanti).
- Lakukan sampling acak dalam masing-masing strata: Setelah terbagi, ambil sampel secara acak dari setiap strata.
Setelah pengambilan sampel, untuk menghitung rata-rata dari seluruh populasi berdasarkan hasil sampel dari setiap strata, digunakan rumus estimasi berikut:
\[
\bar{X}_{st} = \sum_{h=1}^{L} \left(\frac{N_h}{N}\right) \bar{X}_h
\]
Dengan:
- \( \bar{X}_{st} \) = rata-rata populasi secara keseluruhan
- \( N_h \) = jumlah populasi di strata ke-h
- \( N \) = total populasi
- \( \bar{X}_h \) = rata-rata sampel di strata ke-h
Jika sobat ingin menghitung varians dari estimasi tersebut, gunakan rumus berikut:
\[
V(\bar{X}_{st}) = \sum_{h=1}^{L} \left(\frac{N_h^2}{N^2}\right) \left(\frac{S_h^2}{n_h}\right)
\]
Dengan:
- \( S_h^2 \) = varians di strata ke-h
- \( n_h \) = jumlah sampel di strata ke-h
Rumus ini sangat membantu dalam memperkirakan akurasi rata-rata hasil sampling yang dilakukan secara stratifikasi, terutama dalam survei berskala besar yang membutuhkan ketelitian tinggi.
Rumus Rata-rata dan Varians Stratified Sampling
Setelah sobat memahami prosedur stratified sampling, kini saatnya membahas bagaimana menghitung nilai rata-rata dan varians dari sampel yang diambil. Tujuannya tentu untuk memperoleh estimasi yang bisa merepresentasikan populasi dengan baik.
Berikut adalah rumus rata-rata gabungan dari seluruh strata:
\[
\bar{X}_{st} = \sum_{h=1}^{L} \left(\frac{N_h}{N}\right) \bar{X}_h
\]
Keterangan simbol:
- \( \bar{X}_{st} \) = estimasi rata-rata populasi dari sampel stratifikasi
- \( N_h \) = jumlah elemen dalam strata ke-h
- \( N \) = total populasi (jumlah seluruh \( N_h \))
- \( \bar{X}_h \) = rata-rata sampel dari strata ke-h
Untuk memperkirakan seberapa besar variasi data antar strata terhadap estimasi rata-rata, digunakan rumus variansi sebagai berikut:
\[
V(\bar{X}_{st}) = \sum_{h=1}^{L} \left(\frac{N_h^2}{N^2}\right) \left(\frac{S_h^2}{n_h}\right)
\]
Keterangan tambahan:
- \( S_h^2 \) = varians dari sampel pada strata ke-h
- \( n_h \) = jumlah sampel yang diambil dari strata ke-h
Contoh soal sederhana:
Sebuah survei ingin mengetahui rata-rata pengeluaran bulanan mahasiswa dari 3 jurusan: A, B, dan C. Berikut datanya:
| Jurusan | \( N_h \) | \( n_h \) | \( \bar{X}_h \) (Rata-rata) |
|---|---|---|---|
| A | 100 | 20 | 2.000.000 |
| B | 150 | 30 | 2.500.000 |
| C | 50 | 10 | 1.800.000 |
Total populasi \( N = 100 + 150 + 50 = 300 \)
Maka estimasi rata-rata pengeluaran adalah:
\[
\bar{X}_{st} = \left(\frac{100}{300}\right)(2.000.000) + \left(\frac{150}{300}\right)(2.500.000) + \left(\frac{50}{300}\right)(1.800.000)
\]
\[
\bar{X}_{st} = (0.333)(2.000.000) + (0.5)(2.500.000) + (0.167)(1.800.000) = 666.667 + 1.250.000 + 300.000 = 2.216.667
\]
Jadi, estimasi rata-rata pengeluaran bulanan mahasiswa dari ketiga jurusan adalah sekitar Rp2.216.667.
Metode Alokasi Sampel dalam Stratified Sampling
Menentukan berapa banyak sampel yang diambil dari masing-masing strata juga merupakan bagian penting dalam proses stratifikasi. Berikut adalah tiga metode utama dalam alokasi sampel:
- Proposional: Jumlah sampel di setiap strata sebanding dengan ukuran strata tersebut. Misal strata A memiliki 40% dari populasi, maka ia mendapat 40% dari total sampel.
- Disproposional: Jumlah sampel tiap strata dibuat sama besar, tanpa memperhatikan ukuran strata. Cocok jika strata kecil dianggap sangat penting untuk dianalisis.
- Optimum allocation: Jumlah sampel mempertimbangkan ukuran strata dan varians internalnya. Strata dengan varians tinggi mendapat lebih banyak sampel agar hasil lebih stabil.
Memilih metode alokasi yang tepat bergantung pada tujuan penelitian dan informasi awal yang tersedia tentang populasi. Jika varians antar strata sangat berbeda, optimum allocation seringkali memberikan hasil paling efisien.
Perbandingan metode alokasi sampel dalam stratified sampling.
Syarat Pembentukan Strata
Agar hasil dari stratified sampling valid dan representatif, pembentukan strata harus dilakukan dengan hati-hati. Berikut adalah kriteria strata yang baik:
- Homogen di dalam strata: Elemen-elemen dalam strata memiliki karakteristik yang mirip atau sejenis.
- Heterogen antar strata: Perbedaan antar strata harus jelas dan signifikan agar bisa membedakan pengaruh masing-masing kelompok.
- Dapat diidentifikasi secara jelas: Setiap elemen populasi harus dapat diklasifikasikan ke dalam strata yang tepat.
- Tidak tumpang tindih: Satu elemen tidak boleh masuk ke dalam dua strata berbeda. Setiap elemen hanya boleh berada di satu strata saja.
Contoh yang salah: Membagi strata berdasarkan “usia & status pernikahan” secara bersamaan tapi tanpa kejelasan prioritas, sehingga satu orang bisa masuk ke dua strata sekaligus.
Contoh yang benar: Membagi mahasiswa berdasarkan jenjang studi (S1, S2, S3), di mana masing-masing mahasiswa hanya punya satu status yang jelas dan tidak bisa berada di dua kelompok sekaligus.
Kelebihan Metode Stratified Random Sampling
Metode stratified random sampling menawarkan berbagai keunggulan yang membuatnya sangat populer dalam penelitian, khususnya ketika populasi terdiri dari berbagai kelompok berbeda. Berikut beberapa kelebihannya:
- Representasi lebih baik: Karena setiap kelompok dalam populasi mendapatkan alokasi sampel tersendiri, hasil survei jadi lebih mencerminkan keberagaman populasi secara keseluruhan.
- Efisiensi statistik meningkat: Dengan strata yang homogen, variasi data dalam setiap kelompok lebih kecil, sehingga hasil estimasi menjadi lebih stabil dan presisi meningkat.
- Bisa fokus pada kelompok kecil: Metode ini memungkinkan peneliti untuk memastikan bahwa kelompok minoritas yang jumlahnya kecil pun tetap terwakili dalam sampel.
“Metode ini sangat cocok ketika peneliti memiliki data awal tentang populasi yang bisa digunakan untuk membuat strata yang bermakna.”
Kelemahan Metode Stratified Random Sampling
Meskipun sangat bermanfaat, metode ini juga memiliki beberapa tantangan yang perlu diperhatikan sebelum diterapkan:
- Memerlukan informasi populasi lebih detail: Untuk membentuk strata, peneliti harus sudah memiliki data karakteristik seluruh populasi, yang kadang tidak mudah atau mahal diperoleh.
- Rumit jika strata terlalu banyak: Semakin banyak strata yang dibuat, semakin kompleks pengelolaan data dan analisisnya.
- Bisa bias jika strata tidak terbentuk dengan baik: Jika pembentukan strata tidak akurat atau tumpang tindih, maka hasil sampling bisa jadi menyesatkan dan tidak merepresentasikan populasi dengan benar.
Kesimpulan
Sobat, setelah membaca panjang lebar tentang stratified random sampling, kita bisa simpulkan bahwa metode ini merupakan pendekatan yang cerdas dan strategis dalam pengambilan sampel, terutama ketika populasi terdiri dari berbagai kelompok yang berbeda secara signifikan. Dengan memanfaatkan pembagian strata yang tepat, hasil survei jadi lebih akurat, efisien, dan representatif.
Namun tentu saja, metode ini memerlukan persiapan dan informasi awal yang memadai. Tanpa data yang cukup untuk membentuk strata yang tepat, manfaat dari stratifikasi tidak akan maksimal. Maka dari itu, sangat penting bagi peneliti untuk memahami kondisi populasi sebelum menerapkan metode ini.
Kami percaya bahwa dengan memahami metode ini lebih dalam, sobat bisa mengambil keputusan yang lebih bijak dalam merancang penelitian dan menganalisis data. Cobalah praktikkan dalam skenario kecil lebih dulu, lalu kembangkan ke studi yang lebih besar. Semoga bermanfaat dan selamat bereksplorasi di dunia statistik!
📚 Further Reading
- Cochran, W.G. (1977). Sampling Techniques. Wiley.
- Lohr, S. L. (2010). Sampling: Design and Analysis. Brooks/Cole.
- Sugiyono. (2012). Metode Penelitian Kuantitatif Kualitatif dan R&D. Alfabeta.