Sobat Statmat, saat kita belajar matematika—khususnya di jenjang SMA atau awal kuliah—trigonometri jadi salah satu topik yang cukup menantang tapi sangat bermanfaat. Dari mengukur tinggi pohon tanpa harus memanjat, hingga menghitung lintasan satelit, semuanya bisa didekati lewat konsep trigonometri.
Nah, di dalam trigonometri ada satu bagian penting yang sering muncul di soal-soal: identitas trigonometri. Ini adalah kumpulan rumus atau persamaan yang selalu benar untuk semua nilai sudut, dan sangat membantu dalam menyederhanakan ekspresi atau menyelesaikan soal.
Artikel ini akan membimbing sobat untuk mengenal identitas trigonometri secara menyeluruh—mulai dari sejarahnya, pengukuran sudut, berbagai jenis rumus, hingga contoh soal dan pembahasan yang mudah dipahami. Yuk, kita mulai dari awal dan kuasai trigonometri dari fondasinya!
Sejarah Trigonometri
Trigonometri berasal dari dua kata Yunani: trigonon (tiga sudut) dan metron (pengukuran). Sejak awal, ilmu ini memang dikembangkan untuk memahami hubungan antara panjang sisi dan besar sudut dalam segitiga—khususnya segitiga siku-siku.
Catatan awal tentang trigonometri bisa ditelusuri hingga zaman Babilonia (sekitar 300 SM), di mana mereka telah menggunakan tabel sinus untuk menghitung gerakan benda langit. Namun, konsep sinus yang kita kenal sekarang belum muncul saat itu.
Tokoh penting dalam sejarah trigonometri adalah Hipparchus (abad ke-2 SM), yang disebut sebagai “Bapak Trigonometri”. Ia menciptakan tabel kordat dalam lingkaran dan membantu menghubungkan geometri dengan astronomi.
Kemudian, di dunia Islam abad pertengahan, para ilmuwan seperti Al-Battani dan Al-Tusi mengembangkan konsep sinus dan kosinus lebih jauh. Mereka juga memperkenalkan pendekatan sistematis terhadap identitas trigonometri, yang kelak memengaruhi perkembangan matematika Eropa.
Di era modern, tokoh seperti Leonhard Euler (1707–1783) menyatukan trigonometri dengan analisis matematika dan kalkulus. Ia memperkenalkan notasi modern seperti sin, cos, dan identitas trigonometri yang kita gunakan hingga sekarang.
Dari Babilonia ke Eropa, dari segitiga ke sinyal elektronik—trigonometri telah menjelma menjadi bahasa universal untuk memahami ruang dan gelombang.
Pengukuran Sudut
Sebelum masuk ke rumus-rumus identitas trigonometri, sobat perlu paham dulu cara mengukur sudut. Dalam trigonometri, sudut bisa dinyatakan dalam dua satuan utama: derajat dan radian. Keduanya sama-sama valid, tapi digunakan untuk konteks yang berbeda.
Ukuran Derajat
Ukuran derajat (°) adalah satuan sudut yang paling familiar dan banyak digunakan dalam kehidupan sehari-hari. Satu lingkaran penuh terdiri dari 360°. Angka 360 ini berasal dari sistem Babilonia kuno yang menggunakan basis 60, dan karena itu 360 dianggap angka yang “ramah pembagian”.
Beberapa sudut istimewa dalam derajat:
- 90° (seperempat lingkaran)
- 180° (setengah lingkaran)
- 270° (tiga perempat lingkaran)
- 360° (satu lingkaran penuh)
Ukuran Radian
Satuan radian berasal dari konsep panjang busur dalam lingkaran. Satu radian adalah sudut yang dibentuk ketika panjang busur sama dengan jari-jari lingkaran. Dalam satu lingkaran penuh terdapat 2π radian, karena keliling lingkaran adalah 2πr.
Konversi penting antara derajat dan radian:
- 180° = π radian
- 90° = π/2 radian
- 360° = 2π radian
Penggunaan radian sangat umum dalam kalkulus dan fisika karena sifat alaminya yang mempermudah penurunan turunan dan integral fungsi trigonometri.
Gunakan derajat saat membaca arah kompas. Gunakan radian saat menurunkan turunan sinus di kalkulus!
Pengertian Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut dalam segitiga, khususnya segitiga siku-siku. Kata “trigonometri” sendiri berasal dari bahasa Yunani kuno: trigonon (tiga sudut) dan metron (mengukur).
Dalam praktiknya, trigonometri sangat luas penggunaannya—mulai dari teknik sipil, navigasi, astronomi, hingga pemrograman grafis. Di jantung trigonometri terdapat fungsi-fungsi seperti sin(θ), cos(θ), dan tan(θ), yang menggambarkan perbandingan antara panjang sisi dalam segitiga.
Pengertian Identitas Trigonometri
Identitas trigonometri adalah persamaan yang selalu benar untuk semua nilai sudut yang didefinisikan. Identitas ini berfungsi layaknya “rumus tetap” yang memudahkan kita dalam menyederhanakan ekspresi, menyelesaikan soal, atau membuktikan kesamaan dua bentuk trigonometri.
Contoh sederhana identitas trigonometri yang paling terkenal adalah:
\( \sin^2 \theta + \cos^2 \theta = 1 \)
Identitas ini disebut sebagai identitas dasar, dan akan sering sobat temui dalam soal-soal trigonometri, kalkulus, bahkan fisika.
Dengan memahami identitas trigonometri, sobat dapat menyederhanakan ekspresi kompleks menjadi bentuk yang lebih mudah dihitung.
Perbandingan Trigonometri
Perbandingan trigonometri adalah inti dari semua fungsi dasar trigonometri. Perbandingan ini didasarkan pada segitiga siku-siku, di mana salah satu sudut selain sudut siku-siku digunakan sebagai acuan (θ).
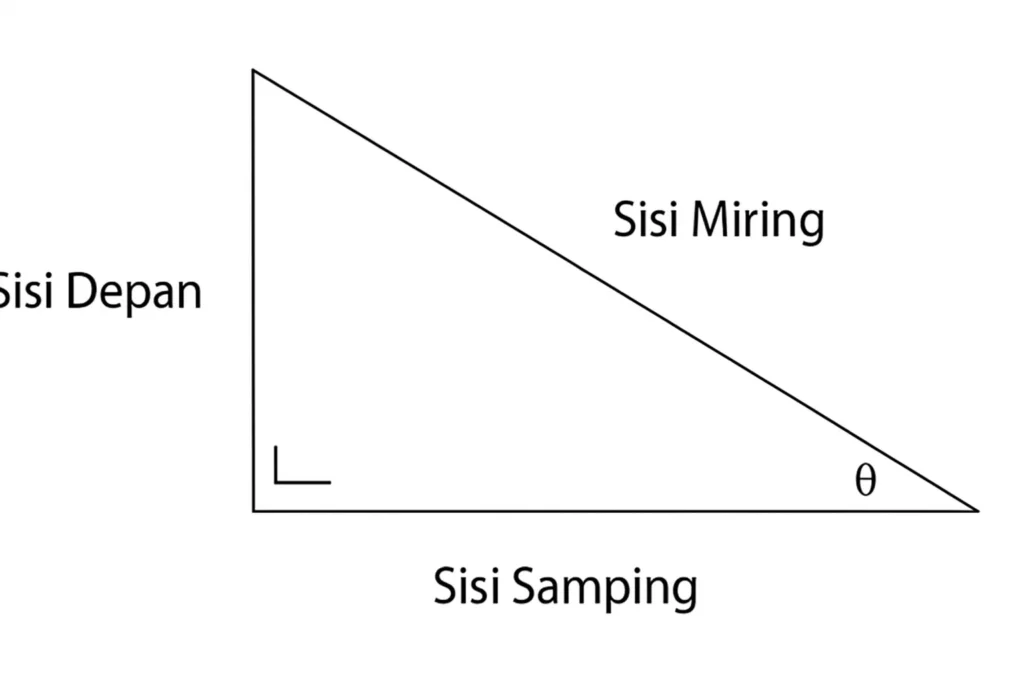
Terdapat enam fungsi utama dalam trigonometri, tapi tiga di antaranya adalah yang paling sering digunakan:
| Fungsi | Definisi | Rumus |
|---|---|---|
| sin(θ) | Sisi depan sudut / sisi miring | \( \frac{\text{opposite}}{\text{hypotenuse}} \) |
| cos(θ) | Sisi samping sudut / sisi miring | \( \frac{\text{adjacent}}{\text{hypotenuse}} \) |
| tan(θ) | Sisi depan sudut / sisi samping | \( \frac{\text{opposite}}{\text{adjacent}} \) |
Tiga fungsi lainnya disebut fungsi kebalikan:
- csc(θ) = 1/sin(θ)
- sec(θ) = 1/cos(θ)
- cot(θ) = 1/tan(θ)
Sebuah cara mudah mengingatnya adalah menggunakan singkatan SOH CAH TOA:
- SOH → Sin = Opposite / Hypotenuse
- CAH → Cos = Adjacent / Hypotenuse
- TOA → Tan = Opposite / Adjacent
Semua identitas trigonometri berakar dari hubungan sederhana segitiga ini. Menguasai perbandingan dasar adalah langkah pertama yang penting.
Macam-macam Rumus Identitas Trigonometri
Setelah memahami perbandingan dasar, sekarang saatnya sobat mengenal berbagai jenis identitas trigonometri. Identitas ini akan sangat berguna dalam menyederhanakan ekspresi, menyelesaikan soal integral, atau membuktikan hubungan antar fungsi.
Identitas Dasar
Identitas dasar adalah pondasi semua bentuk trigonometri lainnya:
- \( \sin^2 \theta + \cos^2 \theta = 1 \)
- \( 1 + \tan^2 \theta = \sec^2 \theta \)
- \( 1 + \cot^2 \theta = \csc^2 \theta \)
Rumus Jumlah dan Selisih Dua Sudut
Digunakan saat sobat ingin menghitung fungsi trigonometri dari jumlah atau selisih dua sudut:
- \( \sin(a \pm b) = \sin a \cos b \pm \cos a \sin b \)
- \( \cos(a \pm b) = \cos a \cos b \mp \sin a \sin b \)
- \( \tan(a \pm b) = \frac{\tan a \pm \tan b}{1 \mp \tan a \tan b} \)
Rumus Sudut Rangkap (Double Angle)
Rumus ini digunakan untuk menghitung fungsi dari sudut 2a:
- \( \sin(2a) = 2\sin a \cos a \)
- \( \cos(2a) = \cos^2 a – \sin^2 a = 2\cos^2 a – 1 = 1 – 2\sin^2 a \)
- \( \tan(2a) = \frac{2\tan a}{1 – \tan^2 a} \)
4.4 Rumus Setengah Sudut
Digunakan saat ingin mencari nilai trigonometri dari sudut a/2:
- \( \sin^2 a = \frac{1 – \cos(2a)}{2} \)
- \( \cos^2 a = \frac{1 + \cos(2a)}{2} \)
- \( \tan^2 a = \frac{1 – \cos(2a)}{1 + \cos(2a)} \)
Rumus Perkalian ke Penjumlahan
Untuk menyederhanakan perkalian dua fungsi menjadi penjumlahan:
- \( \sin a \sin b = \frac{1}{2}[\cos(a – b) – \cos(a + b)] \)
- \( \cos a \cos b = \frac{1}{2}[\cos(a – b) + \cos(a + b)] \)
- \( \sin a \cos b = \frac{1}{2}[\sin(a + b) + \sin(a – b)] \)
Rumus Penjumlahan ke Perkalian
Sebaliknya, digunakan untuk mengubah penjumlahan dua fungsi menjadi bentuk perkalian:
- \( \sin a + \sin b = 2\sin\left(\frac{a + b}{2}\right)\cos\left(\frac{a – b}{2}\right) \)
- \( \sin a – \sin b = 2\cos\left(\frac{a + b}{2}\right)\sin\left(\frac{a – b}{2}\right) \)
- \( \cos a + \cos b = 2\cos\left(\frac{a + b}{2}\right)\cos\left(\frac{a – b}{2}\right) \)
- \( \cos a – \cos b = -2\sin\left(\frac{a + b}{2}\right)\sin\left(\frac{a – b}{2}\right) \)
Sobat nggak harus hafal semua rumus ini sekaligus. Yang penting, pahami konsep dan tahu kapan rumus itu berguna.
Contoh Soal dan Pembahasan
Yuk sobat, kita coba aplikasikan rumus-rumus identitas trigonometri yang sudah kita pelajari tadi. Contoh soal seperti ini sering keluar di ujian sekolah maupun tes masuk perguruan tinggi.
Contoh Soal 1: Sederhanakan ekspresi
Sederhanakan:
\( \frac{1 – \cos(2x)}{2} \)
Pembahasan:
Dari rumus setengah sudut, kita tahu bahwa:
\( \frac{1 – \cos(2x)}{2} = \sin^2 x \)
Jadi, ekspresi tersebut dapat disederhanakan menjadi:
Jawaban: \( \sin^2 x \)
Contoh Soal 2: Buktikan identitas
Buktikan bahwa:
\( \tan(a + b) = \frac{\tan a + \tan b}{1 – \tan a \tan b} \)
Pembahasan:
Gunakan rumus jumlah sudut untuk sinus dan cosinus:
\[
\tan(a + b) = \frac{\sin(a + b)}{\cos(a + b)}
\]
Lalu, gunakan:
\[
\sin(a + b) = \sin a \cos b + \cos a \sin b
\]
\[
\cos(a + b) = \cos a \cos b – \sin a \sin b
\]
Maka:
\[
\tan(a + b) = \frac{\sin a \cos b + \cos a \sin b}{\cos a \cos b – \sin a \sin b}
\]
Bagi pembilang dan penyebut dengan \( \cos a \cos b \):
\[
= \frac{\frac{\sin a}{\cos a} + \frac{\sin b}{\cos b}}{1 – \frac{\sin a}{\cos a} \cdot \frac{\sin b}{\cos b}} = \frac{\tan a + \tan b}{1 – \tan a \tan b}
\]
Terbukti!
Contoh Soal 3: Hitung nilai trigonometri
Jika \( \sin x = \frac{3}{5} \), dan x di kuadran I, hitung nilai \( \cos(2x) \)
Pembahasan:
Diketahui:
\[
\sin x = \frac{3}{5} \Rightarrow \cos x = \sqrt{1 – \sin^2 x} = \sqrt{1 – \frac{9}{25}} = \sqrt{\frac{16}{25}} = \frac{4}{5}
\]
Gunakan rumus:
\[
\cos(2x) = 2\cos^2 x – 1 = 2\left(\frac{4}{5}\right)^2 – 1 = 2\left(\frac{16}{25}\right) – 1 = \frac{32}{25} – 1 = \frac{7}{25}
\]
Jawaban: \( \cos(2x) = \frac{7}{25} \)
Contoh soal seperti ini membantu sobat memahami penerapan identitas dalam bentuk numerik dan pembuktian.
Kesalahan Umum dalam Mengerjakan Soal Trigonometri
Trigonometri bisa jadi momok bagi banyak pelajar, bukan karena konsepnya sulit, tapi karena ada banyak jebakan kecil yang sering tidak disadari. Berikut ini beberapa kesalahan umum yang sering terjadi saat mengerjakan soal identitas trigonometri.
1. Lupa Domain Sudut (Kuadran)
Banyak sobat menghafal rumus tapi lupa memeriksa kuadran sudut. Misalnya, jika diketahui \( \sin \theta = \frac{3}{5} \), maka untuk menentukan \( \cos \theta \), kita perlu tahu apakah sudutnya di kuadran I (positif semua) atau kuadran II (cos negatif). Salah tanda = salah jawaban.
2. Tidak Menggunakan Identitas yang Sesuai
Beberapa soal hanya bisa diselesaikan dengan menggunakan identitas tertentu. Contohnya, ketika ada ekspresi dengan \( \sin^2 x \), banyak yang langsung bingung padahal bisa gunakan identitas \( \sin^2 x = 1 – \cos^2 x \).
3. Langsung Substitusi Angka Tanpa Sederhanakan Dulu
Dalam soal pembuktian identitas, beberapa sobat terlalu cepat memasukkan nilai numerik tanpa menyederhanakan bentuk aljabar terlebih dahulu. Ini bisa membuat proses menjadi panjang dan rumit.
4. Kesalahan Perhitungan Akar dan Pecahan
Misalnya saat menghitung:
\[
\cos x = \sqrt{1 – \sin^2 x}
\]
Sebagian salah dalam proses akar atau lupa bahwa nilai akar bisa ± tergantung kuadran. Selalu cek hasil akhir dan logika dari jawaban.
5. Salah Baca atau Salah Salin Rumus
Rumus-rumus seperti:
\[
\sin(a + b) = \sin a \cos b + \cos a \sin b
\]
sering tertukar jadi minus, atau fungsi tan tertulis sebagai sin, dan sebagainya. Sebaiknya sobat buat daftar rumus identitas dasar di kertas catatan agar bisa dicek sebelum ujian.
Tips dari kami: Jangan hafalkan rumus tanpa mengerti asal-usulnya. Dengan memahami visual dan pembuktian, sobat akan jauh lebih siap mengerjakan soal dengan percaya diri.
Further Reading
- Trigonometry – Lial, Hornsby, Schneider
Buku ini cocok untuk pelajar SMA hingga mahasiswa awal. Penyajian materi sangat sistematis, dilengkapi banyak soal latihan dan pembahasan identitas trigonometri secara mendalam. - Calculus: Early Transcendentals – James Stewart
Jika sobat ingin memahami peran identitas trigonometri dalam integral dan turunan, buku ini wajib dimiliki. Banyak soal melibatkan identitas sudut rangkap, setengah sudut, hingga konversi ke bentuk integral. - Matematika SMA Kelas X–XII – Kurikulum Nasional (Kemendikbud)
Untuk pelajar Indonesia, buku ini memuat topik identitas trigonometri yang sesuai dengan kurikulum dan soal-soal yang sering muncul di UTBK atau ujian nasional.
Kesimpulan
Identitas trigonometri bukan sekadar kumpulan rumus yang harus dihafalkan, tapi merupakan alat penting yang membantu kita memahami dan menyederhanakan hubungan antara sudut dan sisi dalam segitiga. Mulai dari identitas dasar seperti \( \sin^2 \theta + \cos^2 \theta = 1 \) hingga rumus sudut rangkap dan setengah sudut, semuanya memainkan peran vital dalam menyelesaikan soal-soal matematika tingkat menengah hingga lanjut.
Dengan memahami konsep dasar, perbandingan trigonometri, serta bagaimana dan kapan menggunakan masing-masing identitas, sobat akan lebih percaya diri saat menghadapi ujian, tugas sekolah, atau bahkan soal-soal olimpiade. Latihan yang konsisten dan pemahaman visual akan sangat membantu dalam memperkuat logika berpikir matematis sobat.
Kami di Statmat.id percaya bahwa belajar matematika bisa menyenangkan dan tidak perlu bikin stres. Jadi, teruslah eksplorasi, jangan ragu bertanya, dan jadikan identitas trigonometri ini sebagai teman baik dalam perjalanan sobat memahami dunia angka.
Pahami konsep, kuasai rumus, dan jangan takut salah—itulah kunci belajar trigonometri yang sesungguhnya!


