Teorema Pythagoras adalah konsep dasar dalam geometri segitiga siku-siku yang sangat penting dalam matematika dan diterapkan luas dalam kehidupan nyata. Berikut cakupan bahasan artikel ini:
Pengertian Teorema Pythagoras
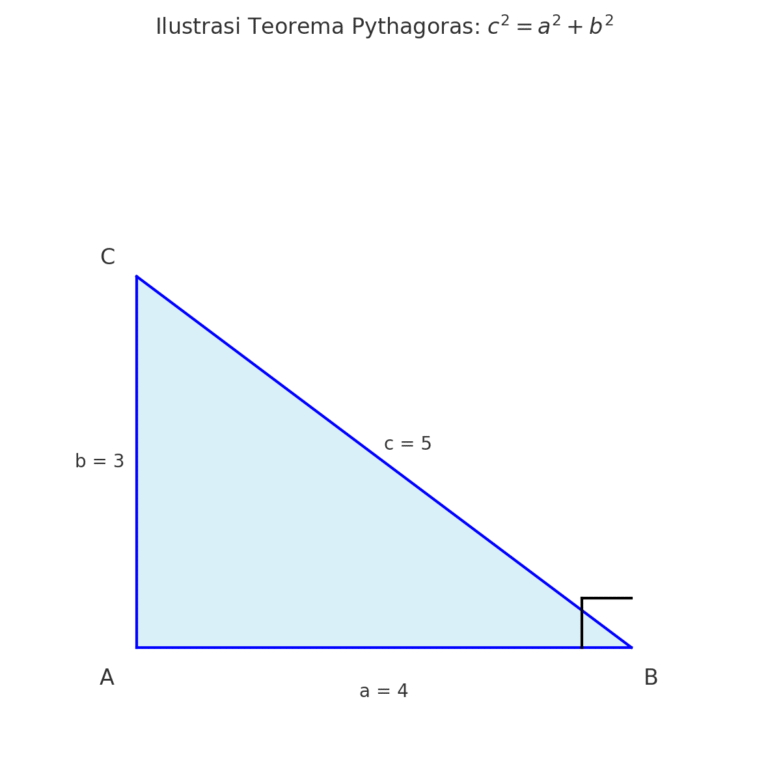
Teorema Pythagoras adalah prinsip yang menyatakan bahwa dalam suatu segitiga siku-siku, kuadrat dari panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat dari kedua sisi lainnya.
Secara matematis ditulis sebagai:
\[ c^2 = a^2 + b^2 \]
Keterangan:
- \( c \) = sisi miring (hipotenusa)
- \( a \) dan \( b \) = sisi-sisi lain yang saling tegak lurus
Hubungan ini hanya berlaku untuk segitiga siku-siku, yaitu segitiga yang memiliki satu sudut 90°.
Sejarah Singkat Teorema Pythagoras
Teorema ini dinamai dari filsuf dan matematikawan Yunani kuno, Pythagoras (570–495 SM), meskipun bukti geometris teorema ini telah digunakan jauh sebelumnya di peradaban Mesopotamia dan Mesir Kuno.
Namun Pythagoraslah yang dianggap sebagai tokoh pertama yang membuktikan secara sistematis bahwa untuk setiap segitiga siku-siku, rumus kuadrat sisi-sisinya berlaku umum.
Rumus Umum dan Bentuk Turunannya
Rumus dasar Teorema Pythagoras adalah:
\[ c^2 = a^2 + b^2 \]
Jika kita ingin mencari salah satu sisi yang bukan hipotenusa, rumus dapat diturunkan menjadi:
-
- Jika ingin mencari sisi \( a \):
\[ a = \sqrt{c^2 – b^2} \]
-
- Jika ingin mencari sisi \( b \):
\[ b = \sqrt{c^2 – a^2} \]
Dalam setiap kasus, pastikan bahwa nilai kuadrat dari sisi miring lebih besar dari nilai kuadrat sisi lainnya agar hasil tetap positif dan masuk akal secara geometri.
Tabel Tripel Pythagoras Umum
Tripel Pythagoras adalah tiga bilangan bulat positif yang memenuhi persamaan Pythagoras. Tabel berikut menunjukkan beberapa tripel yang sering digunakan:
| Sisi A | Sisi B | Sisi C (Hipotenusa) |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
| 11 | 60 | 61 |
Bilangan-bilangan ini sering dipakai untuk mempermudah perhitungan cepat dalam soal matematika atau aplikasi teknis.
Contoh Soal Teorema Pythagoras dan Pembahasannya
Contoh Soal 1
Diketahui sebuah segitiga siku-siku dengan panjang sisi \( a = 6 \) cm dan \( b = 8 \) cm. Hitung panjang sisi miring \( c \).
Penyelesaian:
\[ c^2 = a^2 + b^2 = 6^2 + 8^2 = 36 + 64 = 100 \]
\[ c = \sqrt{100} = 10 \text{ cm} \]
Contoh Soal 2
Diketahui sebuah segitiga siku-siku memiliki hipotenusa \( c = 13 \) cm dan salah satu sisi siku-sikunya \( a = 5 \) cm. Hitung sisi lainnya.
\[ b = \sqrt{c^2 – a^2} = \sqrt{13^2 – 5^2} = \sqrt{169 – 25} = \sqrt{144} = 12 \text{ cm} \]
Contoh Soal 3 (Aplikasi dalam Bangunan)
Sebuah tangga sepanjang 5 meter disandarkan ke dinding. Bagian bawah tangga berjarak 3 meter dari dinding. Berapa tinggi ujung atas tangga dari lantai?
\[ c = 5, a = 3 \Rightarrow b = \sqrt{c^2 – a^2} = \sqrt{25 – 9} = \sqrt{16} = 4 \text{ meter} \]
Penggunaan Teorema Pythagoras dalam Kehidupan Nyata
Teorema Pythagoras banyak digunakan dalam bidang teknik sipil, arsitektur, navigasi, dan bahkan astronomi. Contoh aplikasinya:
- Menentukan panjang diagonal ruangan
- Mengukur jarak terpendek antara dua titik
- Menentukan sudut kemiringan atap bangunan
- Perhitungan lintasan terpendek robot pada bidang dua dimensi
Dalam konstruksi, perhitungan presisi menggunakan tripel Pythagoras sering digunakan untuk memastikan sudut 90 derajat pada struktur seperti fondasi dan dinding.
Perbedaan dengan Rumus Jarak Euclidean
Teorema Pythagoras adalah dasar dari rumus jarak Euclidean dalam bidang dua dimensi.
\[ d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \]
Ini memperluas penggunaan Pythagoras dari geometri murni ke analisis data dan geometri koordinat, seperti dalam klasifikasi data, peta, dan sistem navigasi GPS.
Perluasan ke Dimensi Tiga
Dalam ruang tiga dimensi, teorema Pythagoras diperluas untuk mencari diagonal ruang atau jarak antar dua titik di ruang 3D:
\[ d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2} \]
Contoh: Jika titik A memiliki koordinat (1, 2, 3) dan titik B (4, 6, 9), maka jaraknya:
\[ d = \sqrt{(4 – 1)^2 + (6 – 2)^2 + (9 – 3)^2} = \sqrt{9 + 16 + 36} = \sqrt{61} \]
Penerapan dalam Soal HOTS (Higher Order Thinking Skills)
Soal berbasis Pythagoras juga digunakan dalam asesmen kemampuan berpikir tingkat tinggi. Contoh:
Sebuah taman berbentuk persegi panjang berukuran 12 meter x 5 meter. Seorang anak berjalan dari satu sudut ke sudut berlawanan secara diagonal. Berapa meter ia berjalan?
\[ d = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \text{ meter} \]
Soal seperti ini menuntut pemahaman konsep serta penerapan dalam konteks kehidupan sehari-hari.
Teorema Pythagoras Terbalik
Teorema ini juga digunakan untuk menentukan apakah sebuah segitiga adalah siku-siku, dengan menguji apakah \( c^2 = a^2 + b^2 \).
Contoh: Diketahui panjang sisi segitiga adalah 9 cm, 12 cm, dan 15 cm. Apakah segitiga ini siku-siku?
Uji:
\[ 15^2 = 225 \quad 9^2 + 12^2 = 81 + 144 = 225 \]
Karena nilainya sama, maka segitiga tersebut adalah segitiga siku-siku.
Tips Menghadapi Soal Pythagoras
- Kenali ciri segitiga siku-siku dan kata kunci dalam soal
- Gunakan tripel Pythagoras umum untuk soal cepat
- Selalu perhatikan satuan (cm, meter, dll.)
- Perhatikan konteks jika soal menggunakan skenario nyata (bangunan, taman, tangga, dll.)
Kesimpulan
Teorema Pythagoras bukan hanya bagian penting dari kurikulum matematika, tetapi juga prinsip praktis dalam banyak aspek kehidupan nyata. Dengan memahami konsep, rumus, serta variasi soal yang muncul, siswa dan praktisi dapat menyelesaikan berbagai masalah geometri dengan presisi. Baik dalam bentuk tripel klasik, penerapan dimensi tiga, atau konteks kehidupan sehari-hari, Pythagoras tetap menjadi fondasi penting yang relevan hingga hari ini.