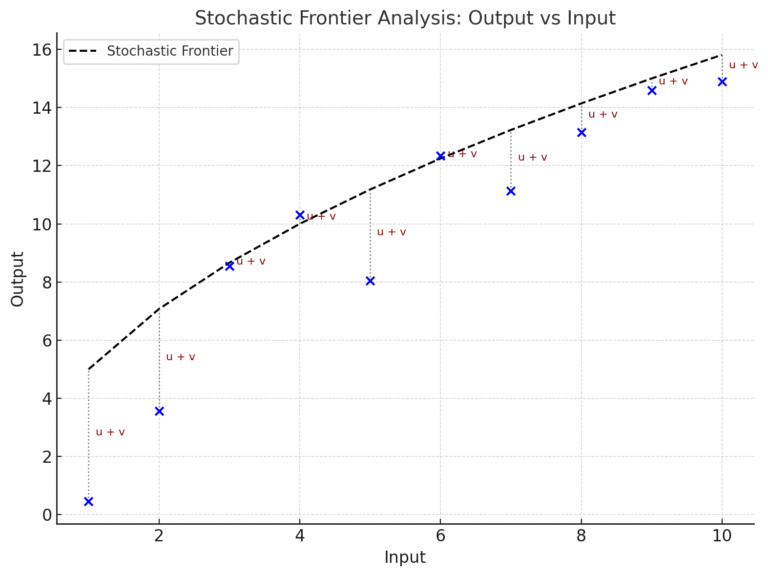
Stochastic Frontier Analysis adalah metode statistik untuk mengukur efisiensi teknis dalam produksi menggunakan pendekatan batas (frontier) stokastik. Teknik ini penting untuk memahami deviasi output dari batas produksi maksimum.
Berikut cakupan bahasan artikel ini:
Pengertian Stochastic Frontier Analysis (SFA)
Stochastic Frontier Analysis (SFA) adalah pendekatan ekonometrik yang digunakan untuk mengestimasi efisiensi teknis unit produksi (seperti perusahaan atau industri) dengan mempertimbangkan kemungkinan adanya kesalahan acak dalam proses produksi. SFA dikembangkan sebagai pengembangan dari metode deterministic frontier yang tidak mempertimbangkan faktor stokastik.
Model frontier mencerminkan batas maksimum output yang dapat dicapai oleh suatu unit produksi dengan input tertentu. Perbedaan antara output aktual dan output maksimum ini ditafsirkan sebagai inefisiensi teknis, ditambah dengan kesalahan acak.
Sejarah dan Perkembangan SFA
Konsep dasar SFA diperkenalkan oleh Aigner, Lovell, dan Schmidt (1977), serta Meeusen dan van den Broeck (1977). Tujuan utamanya adalah memisahkan deviasi output akibat inefisiensi teknis dari deviasi akibat gangguan stokastik. SFA sejak itu berkembang menjadi alat analisis yang banyak digunakan dalam studi ekonomi, pertanian, industri manufaktur, dan sektor publik.
Struktur Umum Model SFA
Model produksi frontier dalam SFA untuk unit ke-i dapat dinyatakan sebagai:
\[ y_i = f(x_i; \beta) \cdot \exp(v_i – u_i) \]
Atau dalam bentuk logaritmik (lebih umum digunakan):
\[ \ln(y_i) = \ln f(x_i; \beta) + v_i – u_i \]
Keterangan:
- \( y_i \) = output dari unit ke-i
- \( x_i \) = vektor input yang digunakan oleh unit ke-i
- \( \beta \) = parameter yang diestimasi
- \( v_i \) = komponen error acak (statistical noise), asumsi \( v_i \sim N(0, \sigma_v^2) \)
- \( u_i \) = komponen inefisiensi, asumsi \( u_i \geq 0 \), sering diasumsikan mengikuti distribusi half-normal \( N^+(0, \sigma_u^2) \)
Komponen Stokastik dalam SFA
Pemisahan dua komponen error dalam SFA menjadi hal mendasar:
- vi menangkap fluktuasi acak yang tidak dapat dikontrol (misalnya cuaca, kesalahan pengukuran)
- ui menangkap inefisiensi teknis dalam proses produksi
Hal ini berbeda dengan model regresi klasik, di mana semua deviasi dianggap sebagai satu error term.
Bentuk Fungsi Produksi dalam SFA
Fungsi produksi dalam model SFA bisa berbagai macam bentuk. Yang paling umum:
Fungsi Produksi Cobb-Douglas
Bentuk log-linear:
\[ \ln(y_i) = \beta_0 + \beta_1 \ln(x_{1i}) + \beta_2 \ln(x_{2i}) + \dots + v_i – u_i \]
Bentuk ini sederhana dan interpretasinya langsung terhadap elastisitas input.
Fungsi Produksi Translog
Lebih fleksibel dari Cobb-Douglas, mengizinkan elastisitas yang tidak konstan:
\[ \ln(y_i) = \beta_0 + \sum_j \beta_j \ln(x_{ji}) + \frac{1}{2} \sum_j \sum_k \beta_{jk} \ln(x_{ji}) \ln(x_{ki}) + v_i – u_i \]
Translog lebih cocok untuk kasus di mana hubungan antara input dan output tidak linier.
Estimasi Parameter Model
Parameter \( \beta \), \( \sigma_u^2 \), dan \( \sigma_v^2 \) diestimasi menggunakan metode Maximum Likelihood Estimation (MLE). Beberapa software seperti STATA, Frontier 4.1, R (package frontier), dan Python menyediakan fungsi untuk estimasi SFA.
Diperlukan asumsi distribusi tertentu untuk \( u_i \) dan \( v_i \) agar fungsi likelihood dapat diturunkan dan dioptimalkan.
Perhitungan Efisiensi Teknis
Setelah model diestimasi, efisiensi teknis (TE) setiap unit dapat dihitung sebagai:
\[ TE_i = \exp(-u_i) \]
Nilai TE berkisar antara 0 dan 1. Semakin mendekati 1, semakin efisien unit tersebut.
Contoh Interpretasi:
- Jika \( u_i = 0.2 \), maka \( TE_i = \exp(-0.2) \approx 0.818 \) → artinya unit tersebut 81.8% efisien
Contoh Soal Ringkas
Misal kita memiliki data produksi padi dari 10 petani. Variabel input: luas lahan (hektar) dan jumlah pupuk (kg). Output: ton padi. Kita estimasi fungsi Cobb-Douglas log-linear:
\[ \ln(y_i) = \beta_0 + \beta_1 \ln(la_i) + \beta_2 \ln(pu_i) + v_i – u_i \]
Setelah estimasi, didapatkan \( u_3 = 0.1 \) untuk petani ke-3. Maka efisiensinya:
\[ TE_3 = \exp(-0.1) \approx 0.905 \]
Interpretasi: Petani ke-3 bekerja dengan efisiensi teknis sekitar 90.5%.
Distribusi Komponen Inefisiensi
Berbagai asumsi distribusi untuk \( u_i \) dapat digunakan:
- Half-normal: \( u_i \sim N^+(0, \sigma_u^2) \)
- Exponential: \( u_i \sim \text{Exp}(\lambda) \)
- Truncated-normal: \( u_i \sim N^+(\mu, \sigma_u^2) \)
Pemilihan distribusi berpengaruh terhadap hasil estimasi efisiensi. Half-normal paling sederhana dan banyak digunakan untuk studi awal.
Model Variasi SFA
Time-varying Efficiency
Dalam model ini, efisiensi teknis berubah seiring waktu:
\[ u_{it} = \exp(-\eta(t – T)) \cdot u_i \]
Dimana \( \eta \) adalah parameter perubahan efisiensi, dan \( T \) adalah tahun akhir.
Panel Data SFA
Untuk data lintas waktu dan individu. Struktur panel memungkinkan estimasi dinamis dan kontrol terhadap efek tetap atau acak.
Perbandingan SFA dengan Metode Lain
| Aspek | SFA | DEA (Data Envelopment Analysis) |
|---|---|---|
| Sifat Model | Parametrik, stokastik | Non-parametrik, deterministik |
| Memisahkan noise | Ya (komponen v) | Tidak |
| Asumsi fungsi produksi | Dibutuhkan (misal Cobb-Douglas) | Tidak dibutuhkan |
| Output | Efisiensi teknis dan model produksi | Efisiensi relatif antar unit |
Kelebihan dan Kekurangan SFA
Kelebihan:
- Memisahkan inefisiensi dari kesalahan acak
- Menghasilkan estimasi fungsi produksi
- Cocok untuk data mikro dan panel
Kekurangan:
- Perlu asumsi distribusi yang kuat
- Model rumit dan estimasi sulit untuk pemula
- Sensitif terhadap spesifikasi fungsi
Penerapan SFA di Berbagai Bidang
- Pertanian: mengukur efisiensi petani berdasarkan input seperti lahan dan pupuk
- Industri: mengukur performa pabrik berdasarkan input mesin dan tenaga kerja
- Kesehatan: efisiensi rumah sakit berdasarkan dokter, perawat, dan tempat tidur
- Pendidikan: efisiensi sekolah berdasarkan guru, dana, dan fasilitas
Kesimpulan
Stochastic Frontier Analysis (SFA) adalah metode statistik yang sangat berguna untuk menganalisis efisiensi teknis dengan mempertimbangkan faktor stokastik. Berbeda dengan metode deterministik seperti DEA, SFA menawarkan keunggulan dalam memisahkan antara kesalahan acak dan inefisiensi nyata. Dalam praktiknya, SFA dapat diterapkan dalam berbagai bidang seperti pertanian, pendidikan, kesehatan, dan industri. Meskipun memerlukan asumsi distribusi dan fungsi produksi yang jelas, kelebihan SFA dalam mengestimasi efisiensi yang lebih realistis menjadikannya metode yang unggul dan banyak digunakan dalam penelitian ekonomi dan kebijakan publik.