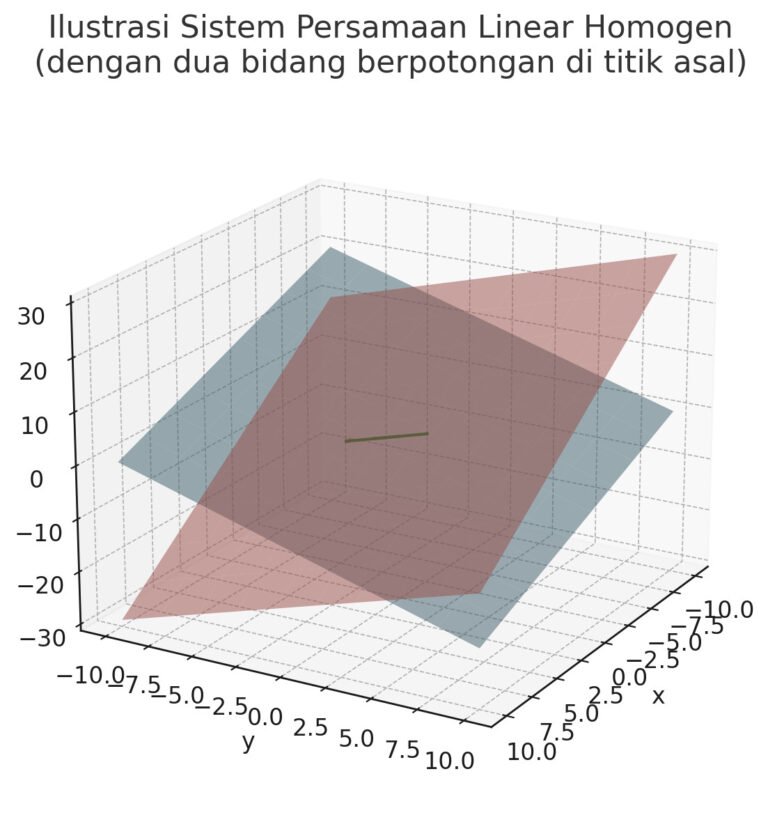
Sistem persamaan linear homogen adalah konsep fundamental dalam aljabar linear yang digunakan untuk memecahkan persoalan dalam berbagai bidang ilmu, seperti teknik, fisika, hingga ilmu komputer. Artikel ini membahas definisi, struktur, sifat, dan metode penyelesaiannya secara mendalam.
Berikut cakupan bahasan artikel ini:
Pengertian Sistem Persamaan Linear Homogen
Sistem persamaan linear homogen adalah sistem persamaan linear yang ruas kanannya semuanya bernilai nol. Dengan kata lain, setiap persamaan dalam sistem tersebut berbentuk:
\[ a_1x_1 + a_2x_2 + \ldots + a_nx_n = 0 \]
di mana \( a_1, a_2, \ldots, a_n \) adalah koefisien bilangan real, dan \( x_1, x_2, \ldots, x_n \) adalah variabel yang akan dicari nilainya.
Contoh sistem persamaan linear homogen:
- \( 2x + 3y – z = 0 \)
- \( -x + y + 4z = 0 \)
- \( 5x – 2y + 2z = 0 \)
Sistem seperti ini disebut homogen karena semua konstanta di sisi kanan persamaan adalah nol. Jika setidaknya satu ruas kanan bukan nol, maka sistem tersebut disebut non-homogen.
Solusi Sistem Homogen
Secara umum, sistem persamaan linear homogen selalu memiliki setidaknya satu solusi, yaitu solusi trivial, di mana semua variabel bernilai nol:
\[ x_1 = x_2 = \ldots = x_n = 0 \]
Namun, sistem ini bisa juga memiliki solusi non-trivial (selain semua variabel nol) tergantung pada struktur koefisiennya.
Kondisi Solusi Non-Trivial
- Jika jumlah persamaan kurang dari jumlah variabel → solusi non-trivial pasti ada.
- Jika jumlah persamaan = jumlah variabel, tetapi koefisien tidak independen secara linear → solusi non-trivial mungkin ada.
Representasi Matriks Sistem Linear Homogen
Sistem persamaan linear homogen dapat direpresentasikan dalam bentuk matriks:
\[ A\vec{x} = \vec{0} \]
di mana:
- \( A \) adalah matriks koefisien berukuran \( m \times n \)
- \( \vec{x} \) adalah vektor kolom variabel \( x_1, x_2, \ldots, x_n \)
- \( \vec{0} \) adalah vektor nol (semua elemen 0) dengan panjang m
Contoh:
Sistem:
- \( x + 2y + 3z = 0 \)
- \( 2x – y + 4z = 0 \)
Representasi matriks:
\[
\begin{bmatrix}
1 & 2 & 3 \\
2 & -1 & 4 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
\end{bmatrix}
\]
Metode Penyelesaian Sistem Homogen
Metode umum yang digunakan untuk menyelesaikan sistem persamaan linear homogen adalah eliminasi Gauss atau Gauss-Jordan. Tujuannya adalah untuk mereduksi sistem menjadi bentuk eselon baris tereduksi agar solusi bisa diperoleh secara sistematis.
Langkah-Langkah Eliminasi Gauss
- Bentuk matriks augmented dari sistem homogen
- Lakukan operasi baris elementer untuk mengubah matriks menjadi bentuk eselon baris
- Tentukan variabel bebas dan nyatakan variabel terikat dalam bentuk variabel bebas
Catatan: Karena sistem homogen selalu memiliki solusi trivial, proses penyelesaian berfokus untuk mencari apakah ada solusi non-trivial.
Contoh Soal dan Penyelesaian
Contoh 1
Selesaikan sistem berikut:
- \( x + 2y + z = 0 \)
- \( 2x + 4y + 2z = 0 \)
Langkah 1: Matriks koefisien
\[
\begin{bmatrix}
1 & 2 & 1 \\
2 & 4 & 2 \\
\end{bmatrix}
\]
Lakukan operasi baris:
- Baris 2 – 2 × Baris 1 → baris kedua menjadi nol
\[
\begin{bmatrix}
1 & 2 & 1 \\
0 & 0 & 0 \\
\end{bmatrix}
\]
Bentuk umum solusi:
- Ambil \( y = t \), \( z = s \) → parameter
- Dari persamaan: \( x = -2t – s \)
Solusi umum:
\[
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
=
t \begin{bmatrix}
-2 \\
1 \\
0 \\
\end{bmatrix}
+
s \begin{bmatrix}
-1 \\
0 \\
1 \\
\end{bmatrix}
\]
Karena ada parameter bebas, sistem memiliki solusi non-trivial.
Sifat-Sifat Sistem Linear Homogen
- Selalu memiliki solusi trivial (nol semua)
- Solusi non-trivial muncul jika jumlah variabel lebih banyak dari jumlah persamaan atau jika persamaan tidak saling independen
- Himpunan solusi sistem homogen membentuk subruang vektor dari ruang vektor \(\mathbb{R}^n\)
Jumlah Solusi dan Rank
Banyaknya solusi non-trivial bergantung pada perbedaan antara jumlah variabel dan rank matriks koefisien.
Rumus:
- Jumlah variabel bebas = \( n – r \)
- \( n \) = jumlah variabel, \( r \) = rank matriks
Jika rank matriks = jumlah variabel → hanya solusi trivial
Jika rank matriks < jumlah variabel → solusi non-trivial (tak hingga solusi)
Perbedaan Sistem Homogen dan Non-Homogen
| Aspek | Homogen | Non-Homogen |
|---|---|---|
| Ruas kanan | Semua nol | Ada yang bukan nol |
| Solusi trivial | Selalu ada | Tidak selalu ada |
| Solusi non-trivial | Mungkin ada (bergantung pada rank) | Bisa unik atau tak hingga |
| Struktur vektor solusi | Subruang vektor | Bukan subruang |
Contoh Aplikasi Sistem Homogen
Sistem homogen banyak diaplikasikan di bidang teknik dan ilmu eksakta:
- Menentukan vektor eigen dalam analisis struktur
- Menemukan kernel dari transformasi linear
- Analisis rangkaian listrik (nodal analysis)
- Teori kontrol (analisis kestabilan sistem)
Tips Memahami Sistem Homogen
- Kuasi visualisasi solusi sebagai garis atau bidang (jika variabelnya dua atau tiga)
- Perhatikan bahwa setiap solusi adalah kombinasi linear dari vektor dasar
- Gunakan representasi matriks untuk menyederhanakan perhitungan
- Latihan dengan berbagai jumlah persamaan dan variabel untuk membedakan kondisi solusi
Kesimpulan
Sistem persamaan linear homogen merupakan bagian penting dari aljabar linear yang sangat kaya akan struktur dan makna geometris. Sistem ini tidak hanya menyajikan solusi matematis tetapi juga memiliki interpretasi vektor dan aplikasi luas di berbagai bidang. Dengan memahami konsep dasar, metode eliminasi, struktur matriks, serta hubungan antara rank dan jumlah solusi, seseorang dapat menguasai dasar-dasar pemodelan sistem linier yang lebih kompleks. Karena selalu memiliki solusi trivial, fokus utama dalam analisis sistem homogen adalah mengidentifikasi kondisi di mana solusi non-trivial muncul dan bagaimana bentuk umum dari solusi tersebut disusun sebagai kombinasi linear. Pemahaman sistem ini juga membuka jalan menuju studi lanjutan seperti teori ruang vektor, eigenvalue-eigenvector, dan transformasi linear.