Limit merupakan konsep fundamental dalam kalkulus yang digunakan untuk memahami perilaku suatu fungsi ketika nilai inputnya mendekati suatu titik tertentu. Konsep ini sangat berguna untuk menganalisis kontinuitas fungsi, turunan, hingga integral.
Salah satu jenis limit yang cukup sering ditemui dalam dunia matematika dan teknik adalah limit tak hingga, yaitu limit yang terjadi ketika nilai variabel mendekati tak hingga (∞) atau menghasilkan nilai tak hingga. Memahami limit tak hingga sangat penting untuk memahami perilaku asimptotik fungsi, grafik kurva, hingga model matematis dalam fisika dan ekonomi.
Pengertian Limit Tak Hingga
Limit tak hingga terjadi ketika nilai x dalam fungsi f(x) mendekati tak hingga (∞ atau −∞), atau ketika hasil dari f(x) itu sendiri menjadi tak hingga. Notasi matematisnya dapat ditulis seperti ini:
\( \lim_{x \to \infty} f(x) \quad \text{atau} \quad \lim_{x \to a} f(x) = \infty \)
Artinya, ketika x mendekati nilai tertentu atau tak hingga, maka hasil dari fungsi tersebut semakin besar tanpa batas. Sebagai contoh:
\( \lim_{x \to \infty} \frac{1}{x} = 0 \)
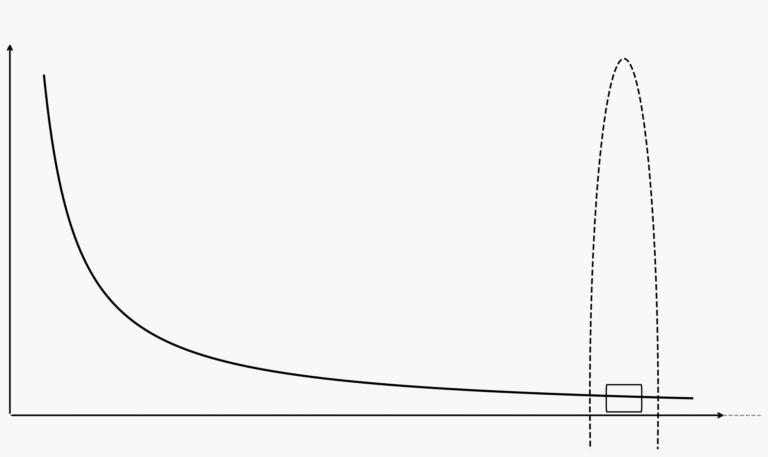
Fungsi 1/x akan semakin kecil dan mendekati nol ketika x menuju tak hingga. Sebaliknya, jika kita punya:
\( \lim_{x \to 0^+} \frac{1}{x} = \infty \)
Artinya, ketika x mendekati nol dari arah kanan, hasil 1/x akan membesar menuju tak hingga. Limit seperti ini penting dalam memahami konsep asimtot vertikal dan horizontal pada grafik fungsi.
Bentuk-Bentuk Tak Tentu (Indeterminate Forms)
Saat menghitung limit tak hingga, sering kali kita menemui bentuk tak tentu yang tidak langsung bisa diselesaikan. Bentuk-bentuk ini disebut indeterminate forms karena tidak bisa disimpulkan secara langsung tanpa manipulasi lanjutan. Berikut beberapa bentuk yang umum:
Bentuk 0/0
Ini adalah bentuk paling klasik dalam limit. Contoh:
\( \lim_{x \to 1} \frac{x^2 – 1}{x – 1} = \frac{0}{0} \)
Untuk menyelesaikannya, kita harus menyederhanakan pecahan tersebut terlebih dahulu.
Bentuk ∞/∞
Bentuk ini muncul ketika pembilang dan penyebut keduanya menuju tak hingga. Contoh:
\( \lim_{x \to \infty} \frac{x^2 + 3x}{2x^2 + 1} = \frac{\infty}{\infty} \)
Dalam kasus seperti ini, pembagian dengan pangkat tertinggi sangat membantu.
Bentuk ∞ – ∞
Bentuk ini muncul pada selisih dua nilai yang sama-sama menuju tak hingga. Contoh:
\( \lim_{x \to \infty} (\sqrt{x^2 + x} – x) = \infty – \infty \)
Pada situasi ini, kita perlu memanipulasi bentuk seperti merasionalkan ekspresi.
Teorema Limit Utama
Teorema limit utama merupakan dasar penting dalam kalkulus, yang memungkinkan kita untuk menyederhanakan dan menghitung limit dari fungsi-fungsi aljabar secara sistematis. Jika f(x) dan g(x) adalah fungsi, serta k adalah konstanta, maka berlaku aturan-aturan berikut:
- Penjumlahan:
\( \lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a} f(x) + \lim_{x \to a} g(x) \)
- Pengurangan:
\( \lim_{x \to a} [f(x) – g(x)] = \lim_{x \to a} f(x) – \lim_{x \to a} g(x) \)
- Perkalian:
\( \lim_{x \to a} [f(x) \cdot g(x)] = \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x) \)
- Pembagian: (dengan syarat \( \lim_{x \to a} g(x) \neq 0 \))
\( \lim_{x \to a} \left[ \frac{f(x)}{g(x)} \right] = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)} \)
- Perkalian dengan konstanta:
\( \lim_{x \to a} [k \cdot f(x)] = k \cdot \lim_{x \to a} f(x) \)
- Pangkat bulat positif:
\( \lim_{x \to a} [f(x)]^n = \left[ \lim_{x \to a} f(x) \right]^n \), dengan \( n \in \mathbb{Z} \)
- Akar fungsi: (dengan \( \lim_{x \to a} f(x) \geq 0 \))
\( \lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)} \)
Teorema-teorema ini digunakan sebagai fondasi dalam banyak perhitungan limit, baik untuk fungsi sederhana maupun fungsi kompleks.
Rumus Cepat dan Teknik Penyelesaian
Penyederhanaan Aljabar
Gunakan faktorisasi, pemfaktoran akar, atau rasionalkan bentuk kompleks. Contoh:
\( \lim_{x \to \infty} (\sqrt{x^2 + x} – x) \)
Gunakan trik perkalian dengan bentuk sekawan untuk menyelesaikan limit ini.
Pembagian dengan Pangkat Tertinggi
Jika ada fungsi polinomial besar, bagi semua suku dengan pangkat tertinggi. Contoh:
\( \lim_{x \to \infty} \frac{x^2 + 5x + 1}{2x^2 – x + 3} = \frac{1 + 5/x + 1/x^2}{2 – 1/x + 3/x^2} \to \frac{1}{2} \)
Aturan L’Hospital
Jika limit menghasilkan bentuk 0/0 atau ∞/∞, maka gunakan:
\( \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)} \)
Syarat: Turunan f(x) dan g(x) harus ada di sekitar titik tersebut. Gunakan berulang jika masih berbentuk tak tentu.
Contoh Soal dan Pembahasan
Soal 1: Limit Bentuk ∞/∞
Hitunglah limit berikut:
\( \lim_{x \to \infty} \frac{3x^2 + 2x + 1}{5x^2 – x} \)
Pembahasan: Gunakan pembagian dengan pangkat tertinggi, yaitu \(x^2\):
\( = \lim_{x \to \infty} \frac{3 + \frac{2}{x} + \frac{1}{x^2}}{5 – \frac{1}{x}} = \frac{3}{5} \)
Soal 2: Limit Bentuk 0/0
Hitunglah:
\( \lim_{x \to 2} \frac{x^2 – 4}{x – 2} \)
Pembahasan:
Faktorkan pembilang:
\( = \lim_{x \to 2} \frac{(x – 2)(x + 2)}{x – 2} = \lim_{x \to 2} x + 2 = 4 \)
Soal 3: Limit Bentuk ∞ – ∞
Hitunglah:
\( \lim_{x \to \infty} (\sqrt{x^2 + x} – x) \)
Pembahasan: Kalikan dengan bentuk sekawan:
\( = \lim_{x \to \infty} \frac{(x^2 + x – x^2)}{\sqrt{x^2 + x} + x} = \lim_{x \to \infty} \frac{x}{\sqrt{x^2 + x} + x} \)
Bagikan pembilang dan penyebut dengan \(x\):
\( = \lim_{x \to \infty} \frac{1}{\sqrt{1 + \frac{1}{x}} + 1} = \frac{1}{2} \)
Latihan Soal Mandiri
- Hitung \( \lim_{x \to \infty} \frac{4x^3 – x}{2x^3 + 3} \)
- Hitung \( \lim_{x \to 0} \frac{\sin x}{x} \)
- Hitung \( \lim_{x \to \infty} \left( \sqrt{x^2 + 4x} – x \right) \)
Coba kerjakan terlebih dahulu, lalu cocokkan dengan pembahasan dari sumber belajar.
Kesalahan Umum
- Melupakan bentuk tak tentu: Tidak mengenali bentuk ∞/∞ atau 0/0 yang butuh manipulasi lebih lanjut.
- Langsung menyubstitusi nilai: Padahal bisa menghasilkan hasil yang keliru.
- Tidak membagi dengan pangkat tertinggi: Sangat penting dalam bentuk limit tak hingga rasional.
- Salah menerapkan aturan L’Hospital: Misalnya pada bentuk yang tidak memenuhi syarat derivatif.
Further Reading
- Khan Academy: Limits and Continuity
- Purcell, Dale Varberg, Calculus with Analytic Geometry, Prentice Hall
Kesimpulan
Limit tak hingga adalah fondasi penting dalam kalkulus, khususnya untuk menganalisis perilaku fungsi saat mendekati nilai ekstrem. Bentuk tak tentu seperti \( \frac{0}{0} \), \( \frac{\infty}{\infty} \), atau \( \infty – \infty \) menantang, tetapi dapat diselesaikan dengan teknik seperti faktorisasi, pembagian dengan pangkat tertinggi, dan aturan L’Hospital.
Pemahaman yang baik terhadap teknik limit ini akan membantu dalam topik lanjutan seperti turunan, integral tak tentu, dan analisis fungsi.