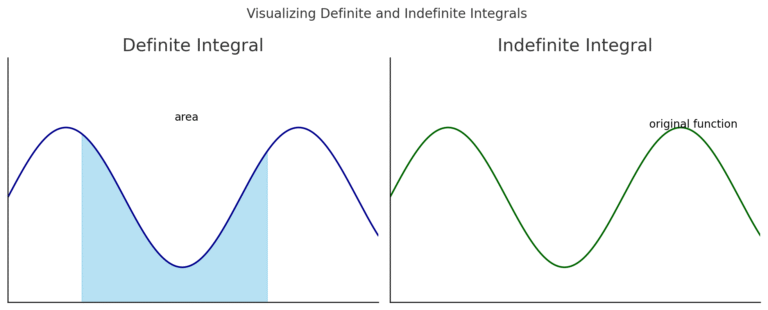
Integral tentu dan integral tak tentu adalah dua konsep penting dalam kalkulus integral yang digunakan untuk menghitung luas, volume, serta menyusun model matematika. Artikel ini mengulas lengkap pengertian, rumus, dan contoh dari kedua jenis integral ini.
Berikut cakupan bahasan artikel ini:
Pengantar Konsep Integral
Integral adalah salah satu pilar utama dalam kalkulus selain turunan. Jika turunan berkaitan dengan laju perubahan, maka integral berhubungan dengan pengukuran luas di bawah kurva, volume, atau akumulasi nilai. Integral digunakan secara luas dalam fisika, teknik, ekonomi, dan bidang ilmu lainnya untuk menghitung total dari besaran yang berubah secara kontinu.
Secara umum, terdapat dua jenis integral yang wajib dipahami dalam kalkulus dasar, yaitu integral tak tentu dan integral tentu. Meskipun keduanya menggunakan notasi integral yang sama, keduanya memiliki makna dan kegunaan yang berbeda.
Pengertian Integral Tak Tentu
Integral tak tentu adalah kebalikan dari proses diferensiasi (turunan). Jika diketahui suatu turunan dari fungsi, maka integral tak tentu digunakan untuk mencari fungsi asalnya. Hasil dari integral tak tentu selalu menghasilkan fungsi umum yang disertai dengan konstanta integrasi.
Notasi umum integral tak tentu:
\[ \int f(x) \, dx = F(x) + C \]
Di mana:
- \( f(x) \) adalah fungsi yang diintegralkan
- \( F(x) \) adalah antiturunan atau fungsi asli dari \( f(x) \)
- \( C \) adalah konstanta integrasi
Aturan dan Sifat Integral Tak Tentu
Berikut beberapa sifat penting dari integral tak tentu yang sering digunakan:
- \( \int k \cdot f(x) \, dx = k \cdot \int f(x) \, dx \) (konstanta dapat dikeluarkan)
- \( \int [f(x) + g(x)] \, dx = \int f(x) \, dx + \int g(x) \, dx \) (integral bersifat distributif)
- \( \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \), dengan \( n \neq -1 \)
- \( \int \frac{1}{x} \, dx = \ln|x| + C \)
- \( \int e^x \, dx = e^x + C \)
- \( \int a^x \, dx = \frac{a^x}{\ln a} + C \), dengan \( a > 0 \) dan \( a \neq 1 \)
Contoh Soal Integral Tak Tentu
Contoh 1
Hitung:
\[ \int (3x^2 + 2x + 1) \, dx \]
Penyelesaian:
\[
\int 3x^2 \, dx + \int 2x \, dx + \int 1 \, dx = x^3 + x^2 + x + C
\]
Contoh 2
Hitung:
\[ \int e^{2x} \, dx \]
Penyelesaian:
\[
\int e^{2x} \, dx = \frac{1}{2} e^{2x} + C
\]
Pengertian Integral Tentu
Integral tentu digunakan untuk menghitung luas di bawah kurva fungsi \( f(x) \) pada selang tertentu [a, b]. Tidak seperti integral tak tentu, integral tentu menghasilkan nilai numerik (bukan fungsi).
Notasi integral tentu:
\[ \int_a^b f(x) \, dx \]
Artinya adalah luas di bawah kurva \( f(x) \) dari titik \( x = a \) hingga \( x = b \).
Aturan dan Rumus Integral Tentu
Integral tentu menggunakan teorema dasar kalkulus yang menghubungkan integral dengan turunan:
\[
\int_a^b f(x) \, dx = F(b) – F(a)
\]
Di mana \( F(x) \) adalah antiturunan dari \( f(x) \).
Sifat-sifat penting:
- \( \int_a^a f(x) \, dx = 0 \)
- \( \int_a^b f(x) \, dx = -\int_b^a f(x) \, dx \)
- \( \int_a^b [f(x) + g(x)] \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx \)
Contoh Soal Integral Tentu
Contoh 1
Hitung:
\[ \int_0^2 (x^2 + 1) \, dx \]
Penyelesaian:
\[
\int_0^2 (x^2 + 1) \, dx = \left[ \frac{x^3}{3} + x \right]_0^2 = \left( \frac{8}{3} + 2 \right) – (0 + 0) = \frac{14}{3}
\]
Contoh 2
Hitung:
\[ \int_1^3 \ln x \, dx \]
Karena tidak dapat diintegralkan secara langsung, gunakan integrasi numerik atau tabel jika tidak diketahui antiturunan eksplisitnya.
Perbedaan Integral Tentu dan Tak Tentu
| Aspek | Integral Tak Tentu | Integral Tentu |
|---|---|---|
| Hasil | Fungsi umum + C | Nilai numerik |
| Notasi | \( \int f(x) \, dx \) | \( \int_a^b f(x) \, dx \) |
| Konstanta integrasi | Ada | Tidak ada |
| Tujuan | Mencari fungsi asal (antiturunan) | Menghitung luas atau akumulasi |
| Batas integral | Tidak ada | Harus ada (a dan b) |
Hubungan Integral dan Turunan
Turunan dan integral adalah proses kebalikan satu sama lain. Jika:
\[ F'(x) = f(x) \Rightarrow \int f(x) \, dx = F(x) + C \]
Dan jika integral tentu digunakan:
\[ \int_a^b f(x) \, dx = F(b) – F(a) \]
Hubungan ini dikenal sebagai Teorema Dasar Kalkulus dan menjadi penghubung utama antara turunan dan integral.
Penggunaan Integral dalam Dunia Nyata
- Menghitung luas bidang tidak beraturan
- Volume benda putar (dengan metode cakram/cincin)
- Akumulasi jumlah dalam fisika (jarak dari kecepatan, gaya dari percepatan)
- Perhitungan probabilitas kumulatif dalam statistik
- Pengukuran total biaya, pendapatan, atau populasi dalam ekonomi
Jenis Fungsi Khusus dalam Integral
- Fungsi eksponensial dan logaritma
- Fungsi trigonometri (sin, cos, tan)
- Fungsi rasional dan irasional
Setiap jenis fungsi memiliki pendekatan integrasi masing-masing, seperti integrasi parsial, substitusi trigonometri, atau pecahan parsial.
Teknik-Teknik Integral Lanjutan (Ringkasan)
- Substitusi: Mengubah variabel untuk menyederhanakan fungsi
- Parsial: Digunakan saat fungsi berbentuk produk dua fungsi
- Pecahan Parsial: Untuk fungsi rasional kompleks
Kesimpulan
Integral tentu dan integral tak tentu merupakan konsep penting dalam kalkulus yang saling melengkapi. Integral tak tentu berguna untuk menemukan fungsi asli dari sebuah turunan, sementara integral tentu digunakan untuk menghitung nilai akumulasi seperti luas dan volume. Pemahaman kedua jenis integral ini tidak hanya penting dalam bidang matematika, tetapi juga sangat berguna dalam penerapan dunia nyata seperti fisika, teknik, ekonomi, dan statistik. Dengan menguasai rumus, sifat, dan teknik perhitungannya, pelajar maupun peneliti dapat menyelesaikan berbagai persoalan numerik dan konseptual yang kompleks secara lebih efektif.