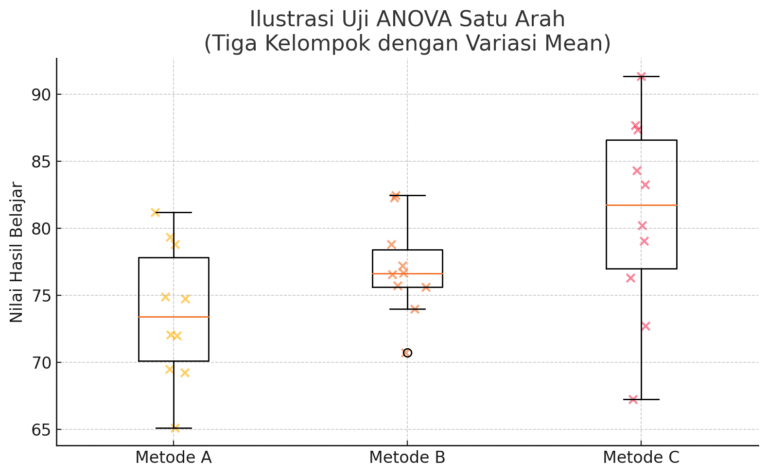
Dalam dunia statistik, kita sering dihadapkan pada situasi di mana kita ingin mengetahui apakah terdapat perbedaan yang signifikan antara beberapa kelompok. Misalnya, apakah rata-rata nilai siswa yang diajar dengan tiga metode pembelajaran berbeda menunjukkan perbedaan? Untuk kasus seperti ini, analisis varians satu arah atau one-way ANOVA merupakan alat yang tepat.
Mengapa tidak cukup hanya menggunakan uji-t? Uji-t hanya membandingkan dua kelompok. Jika kita menggunakan uji-t berulang untuk membandingkan tiga kelompok atau lebih, maka risiko Type I Error (kesalahan menolak hipotesis nol yang benar) akan meningkat. ANOVA mengatasi masalah ini dengan menguji perbedaan rata-rata secara simultan dalam satu uji, sehingga lebih efisien dan akurat.
Kapan Anova Satu Arah Digunakan?
ANOVA satu arah digunakan ketika kita memiliki satu variabel bebas (faktor) dengan dua atau lebih kelompok (level), dan kita ingin mengetahui apakah perbedaan rata-rata antar kelompok tersebut signifikan secara statistik. Contoh umum penggunaannya antara lain:
- Membandingkan rata-rata nilai siswa dari tiga metode pengajaran yang berbeda
- Menguji perbedaan tingkat kepuasan pelanggan berdasarkan jenis layanan
- Menganalisis efektivitas tiga jenis obat terhadap tekanan darah
Yang penting, variabel terikatnya harus berbentuk numerik (interval atau rasio), sedangkan variabel bebasnya berbentuk kategorik.
Asumsi Dasar dalam Anova
Sebelum melakukan uji ANOVA, ada beberapa asumsi dasar yang harus dipenuhi agar hasil uji valid:
- Independensi antar observasi: Setiap data dalam kelompok maupun antar kelompok harus bersifat independen atau tidak saling memengaruhi.
- Distribusi normal: Data dalam masing-masing kelompok harus mengikuti distribusi normal, terutama jika ukuran sampel kecil.
- Homogenitas varians: Varians dari populasi tiap kelompok dianggap sama (homogen). Uji Levene atau Bartlett bisa digunakan untuk menguji asumsi ini.
Jika ketiga asumsi ini tidak terpenuhi, maka hasil uji ANOVA bisa menyesatkan dan alternatif seperti uji Kruskal-Wallis (nonparametrik) mungkin lebih sesuai.
Hipotesis dalam Uji Anova Satu Arah
Dalam uji ANOVA satu arah, kita merumuskan hipotesis sebagai berikut:
- Hipotesis Nol (H0): Semua rata-rata populasi sama, atau tidak ada perbedaan rata-rata antar kelompok.Contoh: μ₁ = μ₂ = μ₃
- Hipotesis Alternatif (H1): Setidaknya ada satu kelompok yang memiliki rata-rata berbeda dari yang lain.
Jika hasil pengujian menunjukkan bahwa perbedaan signifikan, maka kita tolak H₀ dan simpulkan bahwa ada perbedaan rata-rata di antara kelompok.
Notasi dan Matriks Anova Satu Arah
Untuk memahami proses perhitungan ANOVA, penting untuk mengenali beberapa notasi dasar yang digunakan dalam matriks ANOVA:
- k: jumlah kelompok
- n: jumlah total seluruh observasi
- ni: jumlah observasi dalam kelompok ke-i
- \( \bar{X}_i \): rata-rata observasi dalam kelompok ke-i
- \( \bar{X}_T \): rata-rata total semua observasi dari seluruh kelompok
Dari notasi tersebut, kita dapat menghitung beberapa komponen penting:
- SSB (Sum of Squares Between): Mengukur variasi antar kelompok
- SSW (Sum of Squares Within): Mengukur variasi dalam kelompok
- SST (Total Sum of Squares): Total variasi data = SSB + SSW
Setelah nilai-nilai ini dihitung, kita akan membentuk tabel ANOVA untuk menghitung nilai F dan menentukan apakah perbedaan tersebut signifikan.
Prosedur Pengujian Anova
Untuk melakukan uji ANOVA satu arah, terdapat beberapa langkah sistematis yang perlu diikuti. Berikut prosedurnya:
- Hitung jumlah kuadrat antar kelompok (SSB): Mengukur seberapa jauh rata-rata masing-masing kelompok dari rata-rata total.
- Hitung jumlah kuadrat dalam kelompok (SSW): Mengukur seberapa jauh tiap data dalam kelompok dari rata-rata kelompoknya sendiri.
- Hitung total jumlah kuadrat (SST): Total variasi yang merupakan penjumlahan dari SSB dan SSW.
- Buat tabel ANOVA: Tabel ini mencakup nilai SSB, SSW, SST, derajat bebas, dan nilai rata-rata kuadrat.
- Hitung nilai F: Dengan membagi nilai rata-rata kuadrat antar kelompok (MSB) dengan rata-rata kuadrat dalam kelompok (MSW).
Statistik Uji F dan Kriteria Keputusan
Setelah semua nilai kuadrat dihitung, kita gunakan rumus berikut untuk menghitung statistik uji F:
\[ F = \frac{MSB}{MSW} \quad \text{dengan} \quad MSB = \frac{SSB}{k-1}, \quad MSW = \frac{SSW}{n-k} \]
Langkah selanjutnya:
- Tentukan derajat bebas pembilang (df1 = k − 1)
- Tentukan derajat bebas penyebut (df2 = n − k)
- Cari nilai F kritis dari tabel distribusi F sesuai df dan taraf signifikansi (misalnya 0,05)
- Bandingkan F hitung dengan F tabel:
- Jika F hitung ≥ F tabel → tolak H0
- Jika F hitung < F tabel → gagal tolak H0
Contoh Soal Uji Anova Satu Arah
8.1 Penyajian Data
Misalnya kita ingin menguji apakah metode belajar A, B, dan C menghasilkan perbedaan nilai matematika siswa. Berikut data nilai dari masing-masing kelompok:
| Metode A | Metode B | Metode C |
|---|---|---|
| 78 | 72 | 88 |
| 85 | 70 | 90 |
| 82 | 74 | 91 |
8.2 Perhitungan dan Pembentukan Tabel ANOVA
Langkah:
- Hitung rata-rata tiap kelompok
- Hitung rata-rata total
- Hitung SSB, SSW, dan SST
Setelah perhitungan:
| Sumber Variasi | Jumlah Kuadrat (SS) | Derajat Bebas (df) | Mean Square (MS) | F |
|---|---|---|---|---|
| Antar Kelompok (SSB) | XXX | 2 | MSB | F Hitung |
| Dalam Kelompok (SSW) | XXX | 6 | MSW | |
| Total (SST) | XXX | 8 | – | – |
Contoh nilai bisa disesuaikan dengan hasil perhitungan aktual jika diperlukan.
8.3 Pengujian Hipotesis dan Kesimpulan
Setelah kita memperoleh nilai F hitung, kita bandingkan dengan F tabel pada df1 = 2 dan df2 = 6 untuk taraf signifikansi 0,05. Misalnya:
- F hitung = 6.35
- F tabel = 5.14
Nilai tabel nilai F disini:
📥 Tabel F – α = 0.10 (PDF)
📥 Tabel F – α = 0.05 (PDF)
📥 Tabel F – α = 0.01 (PDF)
Karena F hitung > F tabel, maka kita tolak H0 → artinya terdapat perbedaan yang signifikan antara setidaknya satu metode pembelajaran.
Kesimpulan
Uji ANOVA satu arah merupakan metode statistik penting yang digunakan untuk mengetahui perbedaan rata-rata antar lebih dari dua kelompok. Metode ini sangat berguna dalam berbagai penelitian, baik di bidang pendidikan, kesehatan, ekonomi, hingga sosial. Sebelum menggunakan teknik lanjutan seperti ANOVA dua arah atau uji post-hoc, penting untuk memahami prinsip dasar ANOVA satu arah ini dengan baik.
Further Reading
- Sudjana, S. (2005). Metode Statistika. Tarsito.
- Ghozali, I. (2016). Aplikasi Analisis Multivariate dengan SPSS. UNDIP.
- Walpole, R.E. (2012). Introduction to Statistics. Pearson.