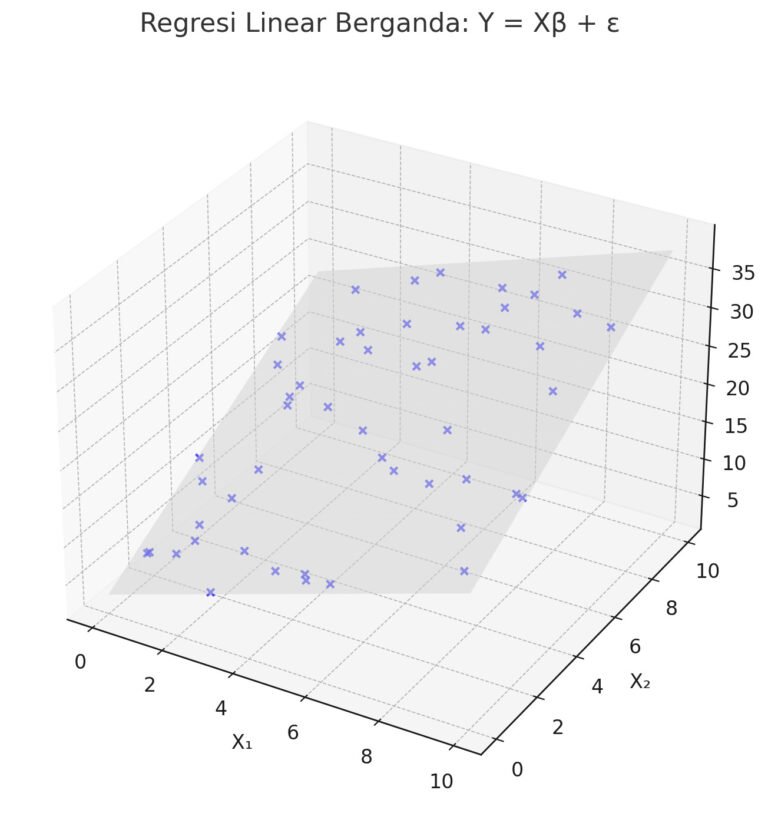
Regresi linear berganda adalah metode statistik penting untuk menganalisis pengaruh dua atau lebih variabel independen terhadap satu variabel dependen. Teknik ini sering digunakan dalam penelitian sosial, ekonomi, pendidikan, dan ilmu alam.
Berikut cakupan bahasan artikel ini:
Pengertian Regresi Linear Berganda
Regresi linear berganda adalah bentuk umum dari analisis regresi yang melibatkan lebih dari satu variabel bebas (independen). Tujuan utamanya adalah memodelkan hubungan linier antara variabel dependen (Y) dan beberapa variabel independen (X1, X2, …, Xn).
Model umum regresi linear berganda dinyatakan dalam persamaan:
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n + \varepsilon \]
Keterangan:
- Y = variabel dependen (yang diprediksi)
- X₁, X₂, …, Xₙ = variabel independen
- β₀ = intersep atau konstanta
- β₁, β₂, …, βₙ = koefisien regresi untuk setiap variabel X
- ε = galat atau error (perbedaan antara nilai observasi dan prediksi)
Perbedaan dengan Regresi Linear Sederhana
Regresi linear sederhana hanya melibatkan satu variabel independen:
\[ Y = \beta_0 + \beta_1 X + \varepsilon \]
Sementara regresi linear berganda menggunakan lebih dari satu variabel X. Kelebihan dari regresi berganda adalah kemampuannya menjelaskan fenomena yang lebih kompleks dan multifaktorial.
Fungsi dan Tujuan Regresi Linear Berganda
- Mengidentifikasi pengaruh simultan beberapa variabel terhadap variabel target
- Membuat model prediksi berbasis variabel bebas yang tersedia
- Mengevaluasi kontribusi masing-masing variabel independen
- Menentukan hubungan kuantitatif antar variabel
Asumsi Dasar Regresi Linear Berganda
Agar hasil analisis valid, beberapa asumsi harus dipenuhi:
- Hubungan Linier: Hubungan antara Y dan setiap Xi bersifat linier
- Normalitas: Residual (ε) menyebar normal
- Homoskedastisitas: Variansi residual harus konstan
- Non-multikolinearitas: Tidak ada korelasi tinggi antar variabel independen
- Independensi: Observasi bersifat independen satu sama lain
Metode Estimasi Koefisien: Least Squares
Koefisien regresi dalam regresi berganda biasanya dihitung dengan Ordinary Least Squares (OLS), yaitu meminimalkan jumlah kuadrat error antara nilai aktual dan nilai prediksi.
Tujuan dari OLS adalah mencari nilai \( \beta_0, \beta_1, …, \beta_n \) yang meminimalkan:
\[ \sum (Y_i – \hat{Y}_i)^2 \]
Dengan \( \hat{Y}_i \) adalah nilai prediksi dari model regresi.
Model regresi linear berganda juga bisa ditulis dalam bentuk matriks:
\[
\mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}
\]
Estimasi koefisien regresi diberikan oleh:
\[
\boldsymbol{\hat{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y}
\]
Keterangan:
- \( \mathbf{X} \) = matriks input variabel independen (dengan kolom pertama berisi 1 untuk intersep)
- \( \mathbf{Y} \) = vektor nilai Y
- \( \boldsymbol{\beta} \) = vektor koefisien regresi
Langkah-Langkah Melakukan Analisis Regresi Linear Berganda
- Definisikan variabel dependen dan independen
- Kumpulkan data
- Periksa asumsi dasar (normalitas, multikolinearitas, dll.)
- Gunakan perangkat lunak statistik (Excel, SPSS, R, Python) untuk menghitung
- Interpretasikan hasil koefisien
- Lakukan uji signifikansi (uji-t dan uji-F)
Contoh Soal Regresi Linear Berganda
Penyajian Data
Seorang peneliti ingin mengetahui pengaruh jam belajar (X₁) dan jumlah latihan soal (X₂) terhadap nilai ujian (Y) siswa. Data 5 siswa disajikan sebagai berikut:
| Siswa | Jam Belajar (X₁) | Latihan Soal (X₂) | Nilai Ujian (Y) |
|---|---|---|---|
| 1 | 2 | 10 | 60 |
| 2 | 3 | 15 | 70 |
| 3 | 4 | 20 | 85 |
| 4 | 5 | 25 | 90 |
| 5 | 6 | 30 | 95 |
Langkah Perhitungan Singkat
Dengan regresi dua variabel X, bentuk modelnya:
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 \]
Hasil estimasi regresi (misalnya setelah dihitung):
\[ Y = 50 + 5X_1 + 0.5X_2 \]
Interpretasi
- Setiap tambahan 1 jam belajar meningkatkan nilai sebesar 5 poin
- Setiap tambahan 1 latihan soal meningkatkan nilai sebesar 0.5 poin
Uji Signifikansi Model
Model regresi harus diuji apakah benar-benar signifikan. Ada dua uji umum:
Uji F (Signifikansi Simultan)
Digunakan untuk mengetahui apakah semua variabel independen secara bersama-sama berpengaruh terhadap Y.
\[ F = \frac{R^2 / k}{(1 – R^2) / (n – k – 1)} \]
Di mana:
- R² = koefisien determinasi
- k = jumlah variabel independen
- n = jumlah observasi
Uji t (Signifikansi Parsial)
Untuk menguji pengaruh masing-masing variabel X terhadap Y:
\[ t = \frac{\hat{\beta}_i}{SE(\hat{\beta}_i)} \]
Bandingkan nilai t hitung dengan t tabel. Jika t hitung lebih besar, maka variabel tersebut signifikan.
Koefisien Determinasi (R²)
Menjelaskan seberapa besar proporsi variasi Y yang dapat dijelaskan oleh semua variabel X:
- R² = 0.90 → berarti 90% variasi nilai Y dijelaskan oleh variabel independen
- Semakin tinggi R², semakin baik model
Multikolinearitas dalam Regresi Berganda
Multikolinearitas adalah keadaan ketika dua atau lebih variabel independen memiliki korelasi tinggi. Ini menyebabkan estimasi koefisien menjadi tidak stabil.
Cara mendeteksi multikolinearitas:
- Melihat nilai Variance Inflation Factor (VIF). Jika VIF > 10 → indikasi multikolinearitas
- Melihat korelasi antar X
Kelebihan dan Kekurangan Regresi Linear Berganda
| Kelebihan | Kekurangan |
|---|---|
| Dapat memodelkan hubungan multivariat | Sensitif terhadap outlier |
| Koefisien mudah diinterpretasi | Membutuhkan asumsi ketat (linier, normal, dll) |
| Digunakan luas dalam berbagai bidang | Tidak cocok untuk hubungan non-linier |
Kesimpulan
Regresi linear berganda adalah alat statistik fundamental dalam menganalisis pengaruh lebih dari satu variabel bebas terhadap variabel dependen. Teknik ini memberikan pemahaman mendalam terhadap hubungan antar variabel dan membantu peneliti dalam prediksi serta pengambilan keputusan. Dengan memahami asumsi, rumus dasar, serta langkah interpretasi model yang benar, kita dapat menggunakan regresi linear berganda secara optimal. Pastikan data memenuhi syarat sebelum digunakan, dan jangan lupa melakukan uji signifikansi serta validasi model agar hasilnya dapat dipercaya.